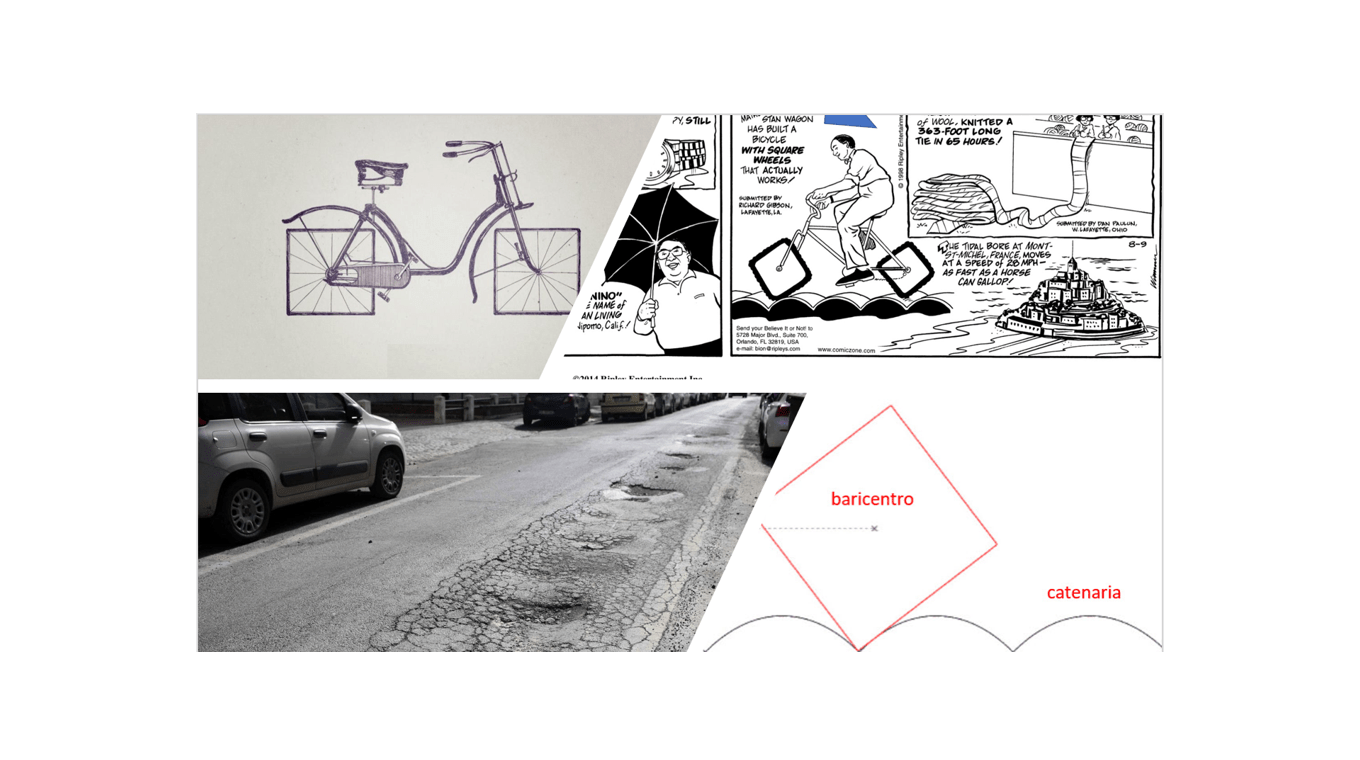
Biciclette e ruote quadrate
di Mario Gentili
Facile è imbattersi nella metafora che associa la ruota quadrata alla volontà di complicarsi la vita, di agire, a dir poco in modo strano.
Difficile, anzi difficilissimo, riuscire a pensare ad una bicicletta a ruote quadrate: prestazioni, praticità, competitività sono caratteristiche che vogliamo dalla nostra bicicletta e quindi… perché le ruote dovrebbero essere quadrate?
La risposta è nella continua e sorprendente curiosità del ricercatore nel chiedersi sempre il perché, o cosa succederebbe se?
Ammettiamolo, quando si pensa ad una ruota le nostre sinapsi si rifiutano di relazionarla ad un quadrato. Si avrebbero difficoltà di utilizzo e sussulti, perché l’altezza del baricentro dal piano di scorrimento varia a seconda che il quadrato sia nella fase della rotazione in cui è appoggiato su un lato o in quella in cui è appoggiato su un vertice.
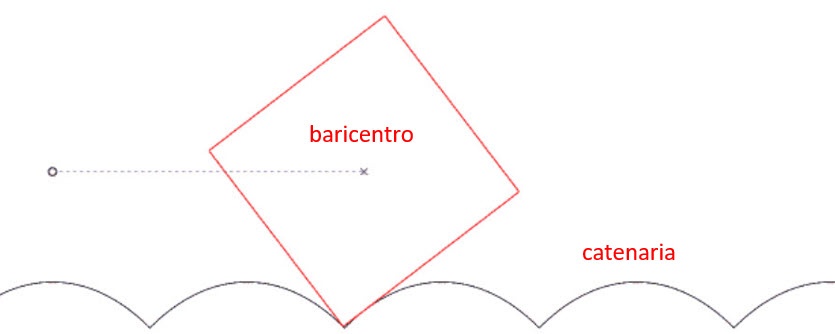
Tuttavia, se si rinuncia alla superficie piana e se ne costruisce una funzionale alla nuova situazione, la ruota quadrata può rotolare con facilità. La superficie si chiama catenaria ed è costituita da una serie di dossi arrotondati.
Il problema è stato più di una volta affrontato dal punto di vista scientifico e matematico. È stato addirittura oggetto della seconda prova dell’esame di maturità scientifica del 2017. Nella traccia ai maturandi veniva chiesto: si può pedalare agevolmente su una bicicletta a ruote quadrate?
L’esigenza
Dando per scontato il principio che la validità di una soluzione non ha caratteristiche universali, ma è strettamente correlata al contesto in cui questa deve essere utilizzata, basta fare soltanto pochi passi indietro nel tempo (rispetto ai tempi della storia) per rendersi conto che non sempre è stato utile avere una ruota rotonda.
Immaginiamo di trovarci nell’antico Egitto dove siamo chiamati a costruire edifici utilizzando pesantissimi blocchi di roccia squadrati. Ebbene, in questo caso la ruota quadrata diventa esigenza!
Quale potrebbe essere il metodo più efficace per fare rotolare i mattoni delle piramidi? I nostri antenati notarono che, se venivano tagliati in più parti dei tronchi di legno, e venivano disposti per terra uno a fianco dell’altro (a formare appunto la sagoma della catenaria), i blocchi potevano rotolare!
Era la prima formulazione e soluzione approssimativa del problema: Se ho qualcosa di quadrato da far rotolare, di che forma deve essere la superficie?
L’approccio scientifico
La tematica fu ripresa da Galileo, e lunga è la lista dei matematici che gli dedicarono giornate di studio: i fratelli Bernoulli, Huygens e Leibniz. Una significativa svolta di rappresentazione matematica si ebbe a metà del ‘700, quando Eulero studiò la curva della catenaria attraverso le equazioni differenziali a variabili separate[1].
L’argomento fu di attrazione anche per filosofi e scrittori. Ad esempio, lo scrittore James Joyce, nell’opera La veglia di Finnegan, nel tentativo di razionalizzare l’irrazionale e insistendo sulla quadratura del cerchio, descrisse a Miss Harriet Shaw Weaver il proprio lavoro in questi termini:
I am really one of the greatest engineers, if not the greatest, in the world besides being a music maker, philosophist and heaps of other things. All the engines I know are wrong. Simplicity. I am making an engine with only one wheel. No spokes of course. The wheel is a perfect square. You see what I’m driving at, don’t you? I am awfully solemn about it, mind you, so you must not think it is a silly story about the mouse and the grapes. No, it’s a wheel, I tell the world. And it’s all square.[2]
Tornando ai giorni nostri, nel 1995 il professore Stan Wagon Last, del dipartimento di Matematica e Computer Science, del Macalester College, St. Paul, Minnesota, assieme al suo team di ricerca, ha realizzato una bicicletta con le ruote quadrate che gli ha permesso di guadagnare una citazione nel Ripley’s Believe It or Not ®, una delle esposizioni mondiali più longeve e di successo che esistano sul pianeta. Qui sotto la simpatica vignetta:
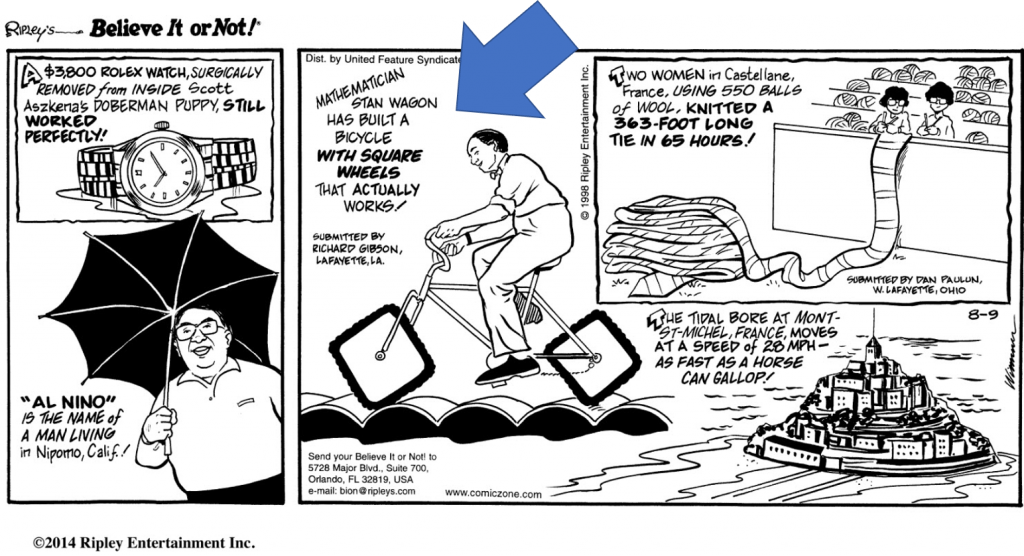
Al prototipo originale, dopo altri 9 anni di ricerca, Stan Wagon ne aggiunse un altro più performante. Nel 2017 un altro matematico, Jason Winckler inventò un veicolo dove le ruote quadrate sono collegate tra loro e mantengono un’inclinazione di circa 22,5°, tale per cui sarebbero in grado di rotolare non solo su una catenaria, ma anche su una superficie piana.
A seguito di tutta questa attenzione ed interesse, la ruota quadrata entra con grande enfasi al MoMtah, il museo nazionale della matematica di New York, dando luogo ad una delle attrazioni più visitate: Pedala nei petali in cui sono presenti degli speciali tricicli sui quali è possibile pedalare in maniera circolare all’interno dei petali di un grande fiore giallo e procedere senza sobbalzi[3].
Applicazioni
Sicuramente abbiamo affrontato male il problema se crediamo che simili studi ed analisi siano condotti solo a scopo speculativo o ludico, e se continuiamo a chiederci… ma a cosa serve?
Di contro, siamo nel giusto spirito della ricerca se ci chiediamo: se avessi una superficie non regolare, quale dovrebbe essere la forma della ruota necessaria a percorrerla? Ovvero, specularmente, se dovessi far rotolare qualcosa che non sia rotondo, quale sarebbe la superficie migliore da realizzare?
Analizzare e risolvere il problema ci permette di realizzare modelli semplificati della realtà che poi possono essere introdotti in soluzioni industriali o di ingegneria per migliorare il nostro tenore di vita.
Per esempio, quale sarebbe la forma migliore per uno pneumatico da competizione per moto? Rotondo sì, ma qual è la sua forma più performante per l’aderenza quando si affronta una curva con la moto inclinata di 60°?
Quale dovrebbe essere il raggio della campata ad arco circolare di un ponte per meglio resistere alle sollecitazioni?
Esperimenti hanno evidenziato che il confronto tra un mezzo con ruote quadrate contro uno normale nell’affrontare una salita ripida ed irregolare ha dato risultati equivalenti tra i due mezzi o a favore della ruota non circolare.
Stan Wagon Last giura che il background degli studi sulla ruota quadrata può essere utilizzato in sistemi micro-elettrici-meccanici (MEMS)[4], ovvero sistemi ‘intelligenti’ che abbinano funzioni elettroniche, di gestione dei fluidi, ottiche, biologiche, chimiche e meccaniche in uno spazio ridottissimo.
Insomma, lo studio della catenaria diventa fondamentale in numerose applicazioni pratiche, anche se non costruiamo più piramidi.
Problemi (e non solo) aperti
Veniamo alla conclusione: potrebbe lo studio sulla catenaria essere utile per percorrere le nostre strade?

Certo avremmo la necessità di conoscere la profondità delle buche, la loro distanza, ma dobbiamo essere fiduciosi: sicuramente la ricerca avrà tempi più brevi di quelli del rifacimento dell’asfalto!
[1] Per i più curiosi, numerosi sono i siti che dedicano spazio all’argomento, tra cui, ad esempio non esaustivo: https://www.youmath.it/lezioni/analisi-due/equazioni-differenziali/629-come-risolvere-le-equazioni-differenziali-a-variabili-separabili.html
[2] Io sono davvero uno dei più grandi ingegneri, se non il più grande, al mondo oltre ad essere un musicista, un filosofo e un mucchio di altre cose. Tutte le macchine che conosco sono sbagliate. Semplicità. Sto costruendo una macchina con una sola ruota. Nessun raggio, naturalmente. La ruota è un quadrato perfetto. Lo vedi a cosa sto mirando, vero? Sono terribilmente serio al riguardo, intendiamoci, quindi non dovete pensare che sia una storia sciocca sul topo e l’uva. No, è una ruota, lo dico al mondo. Ed è tutta quadrata. (traduzione dell’autore).
[3] https://www.youtube.com/watch?v=Ppcgr0zHyx0&feature=youtu.be
[4] Per approfondimenti: https://it.wikipedia.org/wiki/MEMS